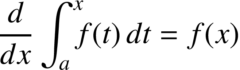[mathjax]
Documentation
Plan de cours 201-NYB H2020- Plan de cours 201-NYB-H2020 version pandémie
- Le plan de cours, avec la pondération des évaluations et une liste de références en lien avec le cours.
-
Page Moodle du cours
- Formulaire sur les limites
- Formulaire de dérivation
- Formulaire d’intégration
- Un formulaire contenant toutes les formules d’intégration supposées connues dans ce cours
Note: les exercices sont tirés du manuel Charron et Parent, Calcul intégral, 5e édition, Chenelière éducation, 2016, ISBN: 978-2-7650-4748-3.
Cours 1
Distribution du Plan de cours.
Quelques rappels sur la dérivée et les limites, introduction à la règle de l’Hospital.
Exercices: pour réviser calcul diffrentiel: p3 Q7, 9, 10, p12 Q1, 2, 3 a) à g),
Dérivation logarithmique: p 13 Q10 et 11.
Règle de l’hospital: p 46 no 1, 2, 3, 4
Cours 2
La règle de l’Hospital s’applique aux formes « (0/0) », « (infty/infty) », ainsi qu’aux limites à droites, à gauche et à l’infini.
Formes indéterminées et « (infty-infty) », « (0cdot infty) », « (0^0) », « (1^infty) » et « (infty^0) »
Exercices: p 46 Q 5, 6, Q7 a) à d), Q8, 9, 10 a), b), Q 11 a) à m)
Récap: p 49 Q20 a) à j), Q25 a) à j)
Cours 3
Équation différentielles, primitives, intégrale indéfinie, formules d’intégration de base.
Distribué en classe: un formulaire d’intégration qui contient toutes les formules d’intégration qui seront supposées connues dans ce cours.
Exercices: p 68 Q1, 2, 3, 4, 5, 6 a) -> j).
Cours 4
Différentielles et changement de variables.
La différentielle d’une fonction (y=f(x)) est définie par $$dy = f'(x) dx.$$ Nous avons vu que la différentielle peut servir à approximer des fonctions de la manière suivante: $$f(a+dx) approx f(a)+dy.$$
La différentielle intervient dans l’utilisation du changement de variable dans les intégrales indéfinies: [int f(g(x)) g'(x) ,dx = int f(u) , du. ]
Exercices: p 79 Q 1 a) -> j), Q 2 a) -> j), Q 3 a) -> j), Q 4 a) -> c), Q 5 a) -> c), Q6, Q7, Q8 a) et b), Q9 a) et b).
Exercices sur la différentielle: p 19 Q1, Q4, Q5.
Cours 5
Introduction aux sommations et à la notation (displaystylesum).
Exercices: p132 Q1 à 4.
Cours 6
Période d’exercices.
Document: NYB H2020 – Formatif 1
Cours 7
Examen 1 (11 février)
Cours 8
Définition de l’intégrale définie, qui donne l’aire sous une courbe:
$$int_a^b f(x), dx = lim_{nto infty} sum_{k=1}^n fleft(x^ast_kright) Delta x_k $$
Exemples de calcul d’aire à l’aide de cette définition.
Propriétés générales de l’intégrale définie.
Devoir 1 à remettre au moment de l’examen 2.
Exercices: p 144 Q1, 3, 4, 5, 7, 9, 10, 11.
Cours 9
La relation entre la dérivée et l’intégrale définie est résumée dans les deux énoncés constituant le théorème fondamental du calcul:
[frac{d}{dx} int_a^x f(t) , dt = f(x) qquad int_a^b f'(x),dx = f(b) – f(a).]
Exercices: p. 144 Q 1,3,5,7,9,10,11
Cours 10
Changement de variable avec les intégrales définies:
[int_a^b f'(g(x))g'(x),dx = int_{g(a)}^{g(b)} f(u),du.]
Applications du théorème fondamental: calcul d’aires.
Exercices: p. 161 Q 1 à 11, et p. 152 Q 2
Cours 11
Intégration par parties: la relation
$$int v , du = uv – int u, dv$$
et ses multiples utilisations pour calculer des intégrales indéfinies.
Nous avons aussi vu l’idée de formule de récurrence: n’apprenez pas par coeur les formules de récurrence!
Exercices: p 211 Q 1,2,3,4,5,6,7 a), 8, 9.
Cours 12
Rappels sur certaines identités trigonométriques comportant les fonctions sinus et cosinus (formulaire de trigo distribué en classe).
Exemples pour illustrer les différentes méthodes d’intégration pour les intégrales comportant les fonctions sinus et cosinus. L’idée générale est d’utiliser les identités trigonométriques pour transformer les intégrales.
Exercices:
Cours 13
Méthodes d’intégration pour les intégrales comportant les fonctions sécantes et tangentes
Variante: intégrales de fonction comportant les fonctions cosécantes et cotangentes.
Mélange de toutes les fonctions trigonométriques: ramener à des fonctions exprimées à l’aide des fonctions sin et cos ou exprimée avec les fonctions sec et tan.
Exercices: p221 Q2, 3, 4, 5 p 250 Q 1 et 2
Cours 14
Période d’exercice
Document: Formatif 2
Pour vous pratiquer à calculer l’aire sous une courbe à l’aide de la définition d’intégrale définie, calculer (int_1^2 (x+1)^2, dx) à l’aide de la définition et de vérifier le résultat à l’aide du théorème fondamental.
Interruption due à la pandémie
L’échéancier qui suit a été modifié
Semaine du 6 avril
Cours 15
Examen 2 (10%) – cet examen a lieu via Moodle : https://moodle.cegep-st-laurent.qc.ca/course/view.php?id=2392
Cours 16
Intégration par substitutions trigonométriques
Lire la section 4.3 du manuel (à partir de la p. 221 du manuel) sauf la substitution de Weierstrass (p.232).
Exercices : p234, Q 1, 2, 3, 4, 5, 6, 7.
Semaine du 13 avril
Cours 17
Exercices
Cours 18
Décomposition en fractions partielles.
Exercice:
Semaine du 20 avril
Cours 19
Exercices
Cours 20
Intégrales impropres
Une intégrale est impropre si la région dont on veut déterminer l’aire n’est pas bornée (ne peut pas être encerclée par un cercle de rayon assez grand). La plupart du temps, les intégrales impropres sont associées à des asymptotes verticales ou horizontales.
Manuel: étudier la section 5.5 p290 à 296
Regarder les 7 premiers vidéos de cette série
Exercices: p302 Question 1, 2 a), b), c), d) 3 a), b), c), d), e) 4 a), b. 5. a) b) c).
Semaine du 27 avril
Cours 21
Période d’exercice
Cours 22
Examen 3 (25%)
Semaine du 4 mai
Cours 23
Présentation des suites et séries.
Document: diaporama présenté en classe.
- Un article sur l’histoire des séries:
- Marc-Antoine Coppo, Une histoire des séries infinies d’Oresme à Euler, La Gazette des Mathématiciens, no. 120. 2009.
Article en ligne sur le site de l’auteur
Manuel: 314 à 318
Exercices: p 326 Q 1,2,3.
Devoir 2 (10%) à remettre à la fin de la session: énoncé sur Moodle, à faire sur le serveur sage du département (voir énoncé)
Cours 24
Somme d’une série géométrique finie:
\[\sum_{k=0}^n Ar^k = \frac{1-r^{n+1}}{1-r}. \]
Série géométrique infinie: si $|r|<1$, alors
\[\sum_{k=0}^\infty Ar^k = lim_{n \to \infty} A\frac{1-r^{n+1}}{1-r} = \frac{A}{1-r}. \]
Diaporama sur les séries géométriques.
Manuel: p 337 à p 343.
Exercices: p 346 Q 4,5,6,7,8,11.
Semaine du 11 mai
Cours 25
Une série de puissance est une série « polynomiale » :
\[\sum_{n=0}^{\infty} a_n (x-a)^n.\]
Diaporama sur les séries de puissances
Exercices:
Cours 26
Séries de Taylor.
La série de Taylor centrée en $x=a$ d’une fonction $f(x)$ est la série de puissance
\[\sum_{n=0}^\infty a_n (x-a)^n \]
où
\[a_n = \frac{f^{(n)}}{n!}.\]
Diaporama sur les séries de Taylor
Exercices:
Examen Formatif 4
Semaine du 18 mai
Cours 27
Période de révision
Cours 28
Examen final (25%). Date limite de remise pour le devoir 2 (10%).