Information pour le cours d’algèbre linéaire et géométrie vectorielle de Yannick Delbecque, session A2024.
- Me contacter/disponibilité
- Plan de cours
- Manuel obligatoire: PAPILLON, V., & ZUCHOWSKI, D. (2011). Vecteurs, matrices et nombres complexes. Groupe Modulo. ISBN : 9782896504664.
Échéancier
1. Présentation du cours. Réduction de Gauss
Fiche – Réduction et algorithme de Gauss
2. Vecteurs, espaces vectoriels et affines.
Manuel sections 1.1. Exercices: 1.1 (p12): Q1 à 17.
3. Combinaison linéaires et bases
Manuel section 1.2. Exercices 1.2 (p 25).
4. Repères et coordonnées
Manuel section 1.3. Exercices 1.3 (p 35).
5. Produit scalaire : longueurs, angles et projections
Manuel chapitre 2. Exercices 2.1 p 50 et 2.2 p 67 (sauf Q12).
6. Systèmes d’équations $2\times 2$: déterminants et théorème de
Cramer.
(et compléments au sujet du produit scalaire : projection orthogonale)
Manuel section 3.1. Exercice 3.1 Q 1 à 11 (et les questions du chapitre 2 qui n’ont pas donnée au dernier cours).
7. Systèmes d’équations $3\times 3$: déterminants et théorème de
Cramer.
Manuel section 3.1 Exercices: Q 12 à 25 (p 102).
8. Produit vectoriel
Manuel section 3.2. Exercice 3.2 (p 113).
9. Période d’exercices
10. Examen 1
11. Présentation du devoir 1.
12. Droites dans $\mathbb{R}^2$ et $\mathbb{R}^3$.
Section 4.1 (p130) Exercices 4.1 (p140 à 143)
13. Plans dans $\mathbb{R}^3$.
Section 4.2 (p 144) Exercices 4.2 (pp 152 à 155).
14. Système d’équations : réduction, forme ERL, rang.
Chapitre 5 (p 159). Exercices 5.1 (pp 173 à 177) et 5.2 (pp 180 et 181).
15. Période de révision.
16. Examen 2
17. Matrices et produit matriciel.
Section 6.1 et ses exercices.
18. Matrices élémentaires et matrices inverses.
Manuel section 6.2 et ses exercices.
19. Déterminent de matrices $n\times n$, propriétés générales des
déterminants.
Manuel section 6.3 et les exercices 1 à 4 de cette section.
20. Matrices adjointes.
Manuel section 6.3 et ses exercices.
21. Application linéaire 1 : représentation matricielle des
transformations linéaires.
Manuel section 7.1 et ses exercices.
Pour voir l’effet d’une application linéaire sur le carré unité. Faire « Evaluate » pour exécuter le code, vous pouvez ensuite modifier les paramètres.
22. Applications linéaires 2 : rotations et symétries, matrices orthogonales.
Manuel section 7.2 et ses exercices.
23. Applications linéaires 3 : valeurs propres et vecteurs propres.
Manuel section 7.4 et ses exercies.
24. Période de révision.
25. Examen 3
26. Introduction aux nombres complexes et à la relation d’Euler.
Section 8.1 et 8.2 et les exercices associés.
27. Théorème fondamental de l’algèbre.
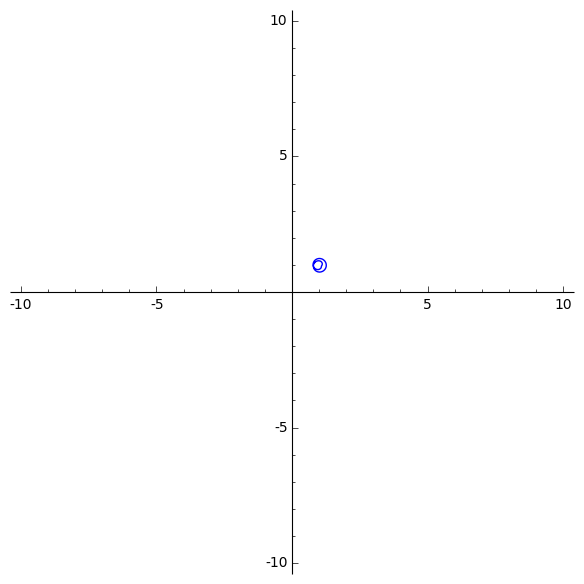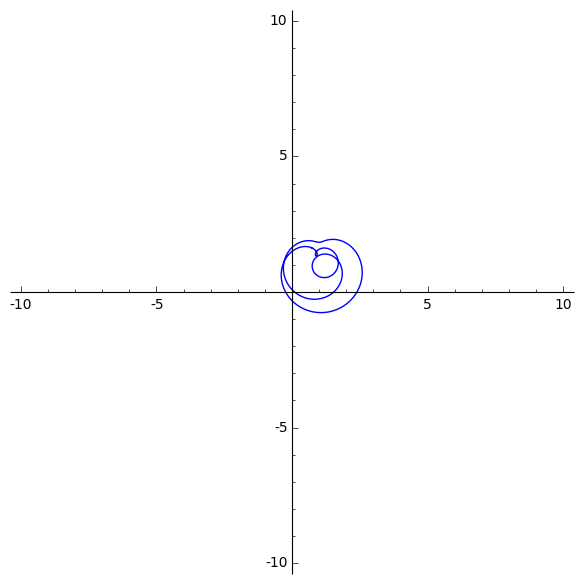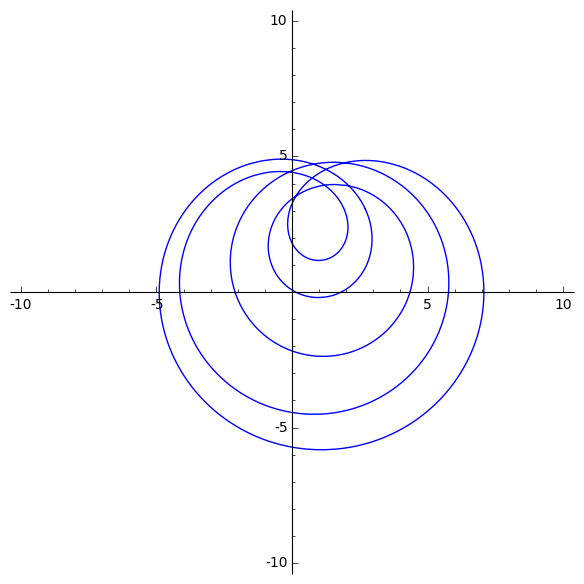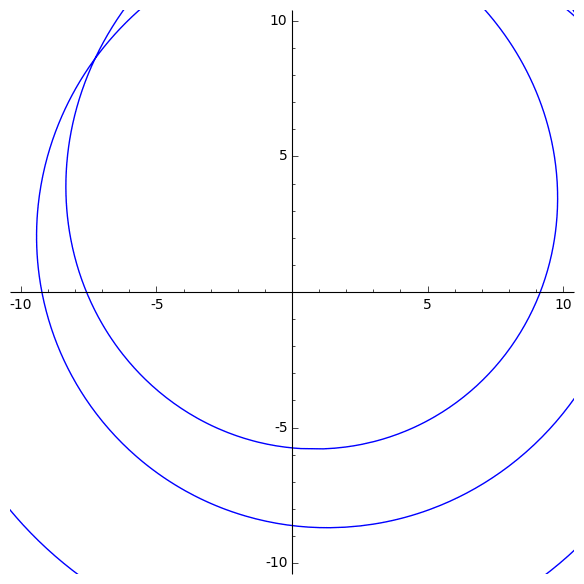
Animation de l’image du cercle complexe de rayon $r$ grandissant par un polynôme de degré 5. Observez que la courbe passe cinq fois par l’origine. Cela implique que le polynôme a cinq zéros.
28. Fonctions complexes.
29. Période de révision.
30. Examen final