Information pour le cours d’algèbre linéaire et géométrie vectorielle de Yannick Delbecque, session H2025.
- Me contacter/disponibilité
- Plan de cours (H2025)
- Manuel obligatoire: PAPILLON, V., & ZUCHOWSKI, D. (2011). Vecteurs, matrices et nombres complexes. Groupe Modulo. ISBN : 9782896504664.
- Outil de révision : Fiches Anki de révision algèbre linéaire(V2) .Ces fiches d’étude seront mise à jour à quelque reprise pendant la session. Ces fiches ont été conçues pour le logiciel Anki , que vous pouvez installer sur toutes les plateformes ou utiliser la version web.
Échéancier
1. Présentation du cours. Réduction de Gauss
Fiche – Réduction et algorithme de Gauss
2. Vecteurs, espaces vectoriels et affines.
Manuel sections 1.1. Exercices : 1.1 (p12): Q1 à 17.
3. Combinaisons linéaires et bases
Manuel section 1.2. Exercices 1.2 (p 25).
Fiche – Indépendance linéaire et bases
4. Repères et coordonnées
Manuel section 1.3. Exercices 1.3 (p 35).
5. Produit scalaire : longueurs, angles et projections
Manuel chapitre 2. Exercices 2.1 p 50 et 2.2 p 67 (sauf Q12).
Fiche – Produits scalaires et angles
6. Systèmes d’équations $2\times 2$: déterminants et théorème de
Cramer.
(et compléments au sujet du produit scalaire : projection orthogonale)
Manuel section 3.1. Exercice 3.1 Q 1 à 11 (et les questions du chapitre 2 qui n’ont pas donnée au dernier cours).
7. Systèmes d’équations $3\times 3$: déterminants et théorème de
Cramer.
Présentation projetée en classe : Cours 7 – Déterminants 3×3
Manuel section 3.1 Exercices : Q 12 à 25 (p 102).
8. Produit vectoriel
Manuel section 3.2. Exercice 3.2 (p 113).
9. Période d’exercices
10. Examen 1
11. Présentation du devoir 1.
Devoir à compléter avant l’examen 3. Il sera ramassé automatiquement dans Cocalc au début de l’examen.
Fiche – Devoir 3D (Document résumant l’aspect mathématique du devoir).
Pour faire le devoir, vous devez vous créer un compte Cocalc, en utilisant l’adresse courriel du collège (qui a la forme No_DA@cegepsl.qc.ca). Le devoir est dans le « projet » Algèbre linéaire qui devrait être présent dans la liste des « projets » de votre compte.
Vous pouvez consulter le Guide cocalc pour cours de programmation qui, bien qu’il s’adresse aux personnes étudiantes de mon cours de programmation qui utilise aussi Cocalc, devrait vous aider à comprendre les bases de l’interface.
12. Droites dans $\mathbb{R}^2$ et $\mathbb{R}^3$.
Section 4.1 (p130) Exercices 4.1 (p140 à 143)
13. Plans dans $\mathbb{R}^3$.
Section 4.2 (p 144) Exercices 4.2 (pp 152 à 155).
14. Système d’équations : réduction, forme ERL, rang.
Fiche – Réduction, pivot, rang
Chapitre 5 (p 159). Exercices 5.1 (pp 173 à 177) et 5.2 (pp 180 et 181).
15. Période de révision.
Formatif 2
16. Examen 2
L’examen 2 aura lieu de lors de la période du lundi 7 avril 2025.
17. Matrices et produit matriciel
Section 6.1 et ses exercices.
18. Matrices élémentaires et matrices inverses.
Manuel section 6.2 et ses exercices.
19. Déterminent de matrices $n\times n$, propriétés générales des
déterminants.
Manuel section 6.3 et les exercices 1 à 4 de cette section.
20. Matrices adjointes.
Manuel section 6.3 et ses exercices.
21. Application linéaire 1 : représentation matricielle des
transformations linéaires.
Manuel section 7.1 et ses exercices.
Pour voir l’effet d’une application linéaire sur le carré unité. Faire « Evaluate » pour exécuter le code, vous pouvez ensuite modifier les paramètres.
22. Applications linéaires 2 : rotations et symétries, matrices orthogonales.
Manuel section 7.2 et ses exercices.
23. Applications linéaires 3 : valeurs propres et vecteurs propres.
(Ce cours est annulé et cette matière ne sera pas à l’Examen 3. Autrement dit, on ira directement au cours 24!)
Manuel section 7.4 et ses exercices.
24. Période de révision.
25. Examen 3
26. Introduction aux nombres complexes et à la relation d’Euler.
Section 8.1 et 8.2 et les exercices associés.
27. Théorème fondamental de l’algèbre.
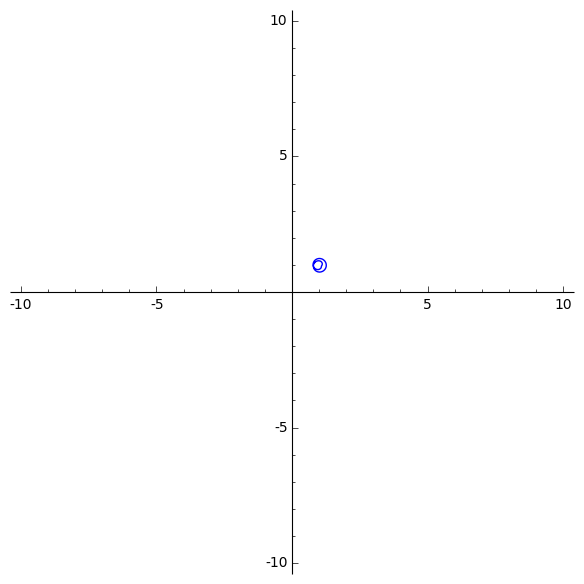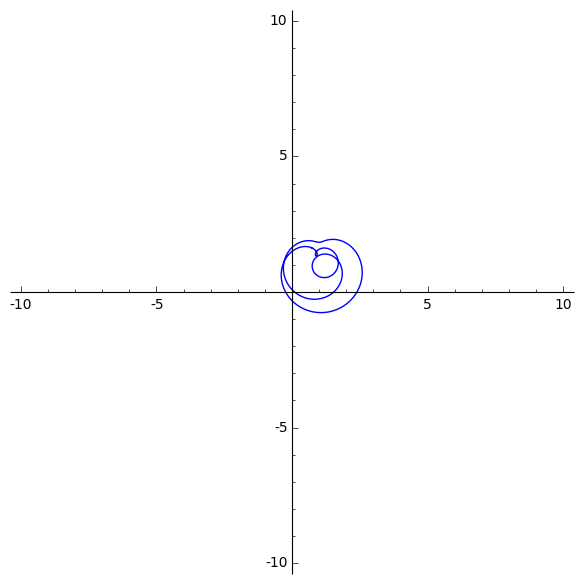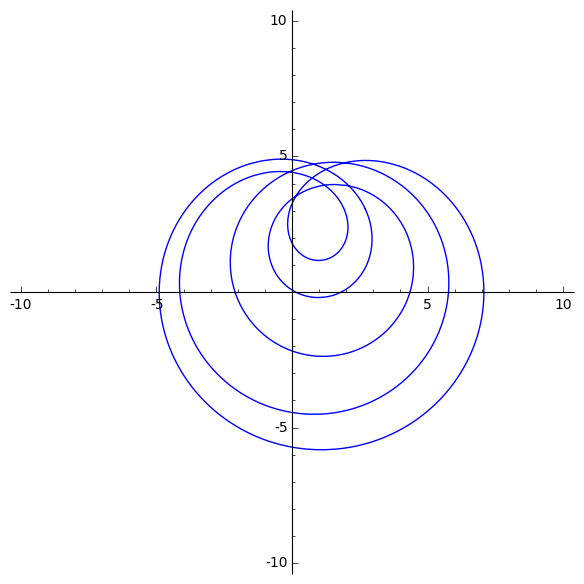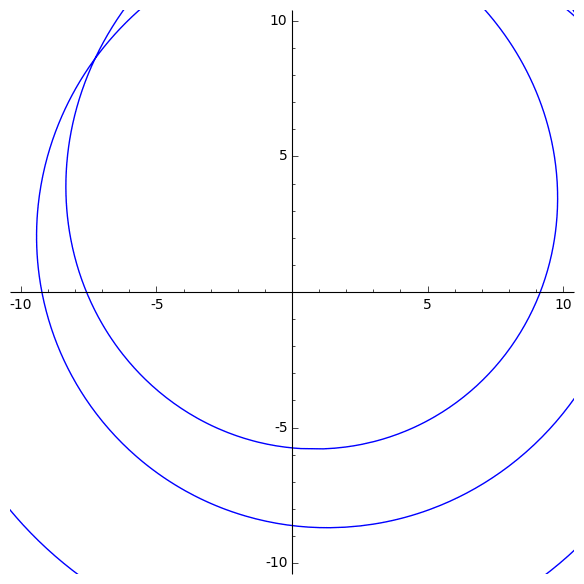
Animation de l’image du cercle complexe de rayon $r$ grandissant par un polynôme de degré 5. Observez que la courbe passe cinq fois par l’origine. Cela implique que le polynôme a cinq zéros.
Section 8.3 et ses exercices.
28. Fonctions complexes.
Section 8.4 et ses exercices.
29. Période de révision.
Formatif final
30. Examen final